

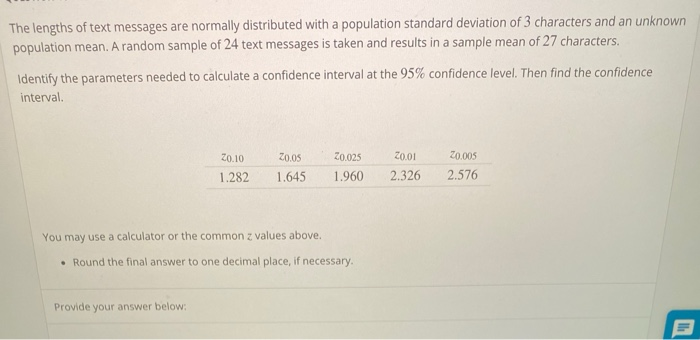
The Student's-t distribution has more probability in its tails than the Standard Normal distribution because the spread of the t distribution is greater than the spread of the Standard.The mean for the Student's-t distribution is 0 and the distribution is symmetric about 0.The graph for the Student's-t distribution is similar to the Standard Normal curve.Properties of the Student's-t Distribution We call the number n − 1 the degrees of freedom ( df ). The other n − 1 deviationsĬan change or vary freely. Because the sum of the deviations isĠ, we can find the last deviation once we know the other n − 1 deviations. In Chapter 2, we used n deviations ( values) to calculate s. The degrees of freedom, n − 1, come from the calculation of the sample standard deviation s. It measures how far is from its mean µ.įor each sample size n, there is a different Student's-t distribution. The t-score has the same interpretation as If you draw a simple random sample of size n from a population that has approximately a normal distribution with mean µ and unknown population standard deviation σ and calculate the t-scoreĪ Student's-t distribution with n − 1 degrees of freedom. With the common use of graphing calculators and computers, the practice is to use the Student's-t distribution whenever s is used as an estimate for σ. Up until the mid 1970s, some statisticians used the normal distribution approximation for large sample sizes and only used the Student's-t distribution for sample The name comes from the fact that Gosset wrote under This problem led him to "discover" what is called the Student's-t distribution. He realized that he could not use a normal distribution for the calculation he found that the actual distributionĭepends on the sample size. Produce accurate results when he tried to calculate a confidence interval. His experiments with hops and barley produced very few samples. Gossett (1876-1937) of the Guinness brewery in Dublin, Ireland ran into this problem. A small sample size caused inaccuracies in the confidence interval. However, statisticians ran into problems when the sample size was small.
Used the sample standard deviation s as an estimate for σ and proceeded as before to calculate a confidence interval with closeĮnough results.
In the past, when the sample size was large, this did not present a problem to statisticians.
Unknown population standard calculator for free#
Download for free at practice, we rarely know the population standard deviation. Available under Creative Commons-ShareAlike 4.0 International License.


 0 kommentar(er)
0 kommentar(er)
